Javascript实现八大排序
排序算法,分为内部排序和外部排序。内部排序要使用内存,而外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。这里只探讨内部排序。
- 交换排序:冒泡排序和快速排序
- 插入排序:直接插入排序和希尔排序
- 选择排序:简单选择排序和堆排序
- 归并排序
- 基数排序
当n较大,则应采用时间复杂度为O(nlog2n)的排序方法:快速排序、堆排序或归并排序序。
快速排序:是目前基于比较的内部排序中被认为是最好的方法,当待排序的关键字是随机分布时,快速排序的平均时间最短。
1.冒泡排序
- 原理:临近的数字两两进行比较,按照从小到大或者从大到小的顺序进行交换,这样一趟过去后,最大或最小的数字被交换到了最后一位,然后再从头开始进行两两比较交换,直到倒数第二位时结束
- 时间复杂度:平均情况:O(n2) 最好情况:O(n) 最坏情况:O(n2)
- 空间复杂度:O(1)
- 稳定性:稳定12345678910111213function bubbleSort(arr){var i = j = 0;for(i=1;i<arr.length;i++){for(j=0;j<=arr.length-i;j++){var temp = 0;if(arr[j]>arr[j+1]){temp = arr[j];arr[j] = arr[j+1];arr[j+1] = temp;}}}}
2.快速排序
- 原理:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
- 时间复杂度:平均情况:O(nlog2n) 最好情况:O(nlog2n) 最坏情况:O(n2)
- 空间复杂度:O(nlog2n)
- 稳定性:不稳定
|
|
3.直接插入排序
- 原理:将一个记录插入到已排序好的有序表中,从而得到一个新,记录数增1的有序表。即:先将序列的第1个记录看成是一个有序的子序列,然后从第2个记录逐个进行插入,直至整个序列有序为止。 比冒泡法和选择排序的性能要更好一些
- 时间复杂度:平均情况:O(n2) 最好情况:O(n) 最坏情况:O(n2)
- 空间复杂度:O(1)
- 稳定性:稳定
要点:设立哨兵,作为临时存储和判断数组边界之用。
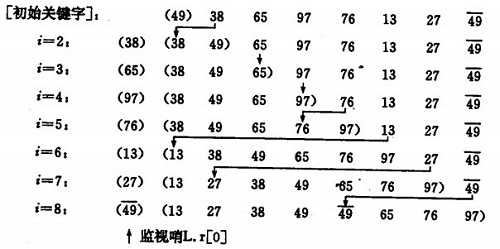
如果碰见一个和插入元素相等的,那么插入元素把想插入的元素放在相等元素的后面。所以,相等元素的前后顺序没有改变,从原无序序列出去的顺序就是排好序后的顺序,所以插入排序是稳定的。
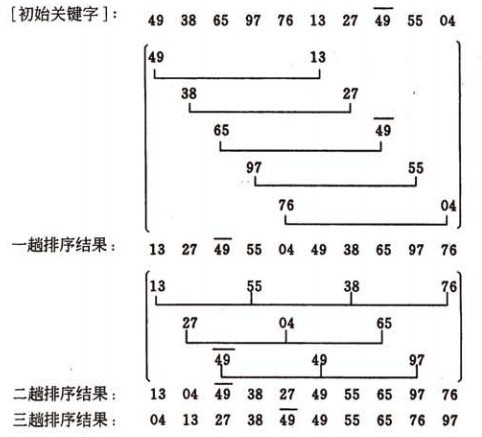
4.希尔排序
- 原理:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行依次直接插入排序。。
- 时间复杂度:平均情况:O(n√n) 最好情况:O(nlog2n) 最坏情况:O(n2)
- 空间复杂度:O(1)
- 稳定性:不稳定
操作方法:
- 选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;
- 按增量序列个数k,对序列进行k 趟排序;
- 每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
5.简单选择排序
- 原理:通过n-i次关键字之间的比较,从n-i+1 个记录中选择关键字最小的记录,并和第i(1<=i<=n)个记录交换 简单选择排序的性能要略优于冒泡排序
- 时间复杂度:平均情况:O(n2) 最好情况:O(n) 最坏情况:O(n2)
- 空间复杂度:O(1)
- 稳定性:不稳定
|
|
6.堆排序
- 原理:堆排序就是利用堆进行排序的方法.基本思想是:将待排序的序列构造成一个大顶堆.此时,整个序列的最大值就是堆顶 的根结点.将它移走(其实就是将其与堆数组的末尾元素交换, 此时末尾元素就是最大值),然后将剩余的n-1个序列重新构造成一个堆,这样就会得到n个元素的次大值.如此反复执行,便能得到一个有序序列了
- 时间复杂度:平均情况:O(nlog2n) 最好情况:O(nlog2n) 最坏情况:O(nlog2n)
- 空间复杂度:O(1)
- 稳定性:不稳定
|
|
7.二路归并
- 原理:假设初始序列含有n个记录,则可以看成n个有序的子序列,每个子序列的长度为1,然后两两归并,得到(不小于n/2的最小整数)个长度为2或1的有序子序列,再两两归并,…如此重复,直至得到一个长度为n的有序序列为止
- 时间复杂度:平均情况:O(nlog2n) 最好情况:O(nlog2n) 最坏情况:O(nlog2n)
- 空间复杂度:O(1)
- 稳定性:稳定
将两个按值有序序列合并成一个按值有序序列,则称之为二路归并排序。
|
|
8.基数排序
- 原理:将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数。
- 时间复杂度:平均情况:O(d(r+n)) 最好情况:O(d(n+rd)) 最坏情况:O(d(r+n)) r:关键字的基数 d:长度 n:关键字个数
- 空间复杂度:O(rd+n)
- 稳定性:稳定
9.排序总结

说明:
- 当原表有序或基本有序时,直接插入排序和冒泡排序将大大减少比较次数和移动记录的次数,时间复杂度可降至O(n);
- 而快速排序则相反,当原表基本有序时,将蜕化为冒泡排序,时间复杂度提高为O(n2);
- 原表是否有序,对简单选择排序、堆排序、归并排序和基数排序的时间复杂度影响不大。
- 稳定性:
- 排序算法的稳定性: 若待排序的序列中,存在多个具有相同关键字的记录,经过排序, 这些记录的相对次序保持不变,则称该算法是稳定的;若经排序后,记录的相对 次序发生了改变,则称该算法是不稳定的。
- 稳定性的好处:排序算法如果是稳定的,那么从一个键上排序,然后再从另一个键上排序,第一个键排序的结果可以为第二个键排序所用。基数排序就是这样,先按低位排序,逐次按高位排序,低位相同的元素其顺序再高位也相同时是不会改变的。另外,如果排序算法稳定,可以避免多余的比较;
- 稳定的排序算法:冒泡排序、插入排序、归并排序和基数排序
- 不是稳定的排序算法:选择排序、快速排序、希尔排序、堆排序
10.选择排序算法准则
每种排序算法都各有优缺点。因此,在实用时需根据不同情况适当选用,甚至可以将多种方法结合起来使用。
一般而言,需要考虑的因素有以下四点:
- 待排序的记录数目n的大小;
- 记录本身数据量的大小,也就是记录中除关键字外的其他信息量的大小;
- 关键字的结构及其分布情况;
- 对排序稳定性的要求。
设待排序元素的个数为n:
- 当n较大,则应采用时间复杂度为O(nlog2n)的排序方法:快速排序、堆排序或归并排序序。
- 快速排序:是目前基于比较的内部排序中被认为是最好的方法,当待排序的关键字是随机分布时,快速排序的平均时间最短;
- 堆排序 : 如果内存空间允许且要求稳定性的,
- 归并排序:它有一定数量的数据移动,所以我们可能过与插入排序组合,先获得一定长度的序列,然后再合并,在效率上将有所提高。
- 当n较大,内存空间允许,且要求稳定性 =》归并排序
- 当n较小,可采用直接插入或直接选择排序。
直接插入排序:当元素分布有序,直接插入排序将大大减少比较次数和移动记录的次数。
直接选择排序 :元素分布有序,如果不要求稳定性,选择直接选择排序 - 一般不使用或不直接使用传统的冒泡排序。
- 基数排序
查找
1.二分查找
二分查找又称折半查找,是在有序数组查找中用到的较为频繁的一种算法,优点是比较次数少,查找速度快,平均性能好;其缺点是要求待查表为有序表,且插入删除困难。
非递归实现
|
|
递归实现
|
|